Algoritmos de Búsqueda en Grafos: Métodos y Aplicaciones

Los algoritmos de búsqueda en grafos son fundamentales en el campo de la informática y la teoría de grafos, permitiendo resolver problemas complejos de manera eficiente. Con el crecimiento exponencial de la información y la necesidad de encontrar rutas, conexiones y patrones en estructuras de datos interconectadas, el estudio de estos algoritmos se ha vuelto más relevante que nunca. Desde la búsqueda de caminos más cortos en redes de transporte hasta la resolución de problemas de optimización en informática, los algoritmos desempeñan un papel crucial.

Este artículo se propone explorar en profundidad los diferentes tipos de algoritmos de búsqueda en grafos, así como sus aplicaciones en el mundo real. Comenzaremos analizando qué son los grafos y cómo se estructuran, seguido de una revisión exhaustiva de los algoritmos de búsqueda más utilizados, como el algoritmo de búsqueda en profundidad (DFS) y el algoritmo de búsqueda en amplitud (BFS). También examinaremos las optimizaciones y variaciones de estos métodos, y analizaremos diversas aplicaciones prácticas en diferentes dominios.

¿Qué son los Grafos?

Un grafo es una estructura matemática que se utiliza para modelar relaciones entre objetos. Un grafo está compuesto por un conjunto de nodos o vértices y un conjunto de aristas que conectan pares de nodos. Este modelo permite representar una amplia gama de problemas en áreas como computación, biología, sociología y logística. Por ejemplo, en las redes sociales, los nodos pueden representar usuarios y las aristas las conexiones o interacciones entre ellos.

Existen diferentes tipos de grafos, como los grafos dirigidos y no dirigidos, los grafos ponderados y no ponderados, y los ciclos y acíclicos. Cada tipo de grafo tiene características únicas que determinan qué tipo de algoritmos de búsqueda son más adecuados para su análisis. Esto resulta crucial cuando se considera qué camino utilizar para encontrar soluciones óptimas en diversas aplicaciones.

Algoritmos de Búsqueda en Grafos

Los algoritmos de búsqueda en grafos son procedimientos utilizados para explorar nodos y aristas en un grafo. Dos de los métodos más conocidos son el algoritmo de búsqueda en profundidad (DFS) y el algoritmo de búsqueda en amplitud (BFS). Ambos algoritmos tienen enfoques y propiedades distintivas, lo que los hace adecuados para diferentes tipos de problemas.

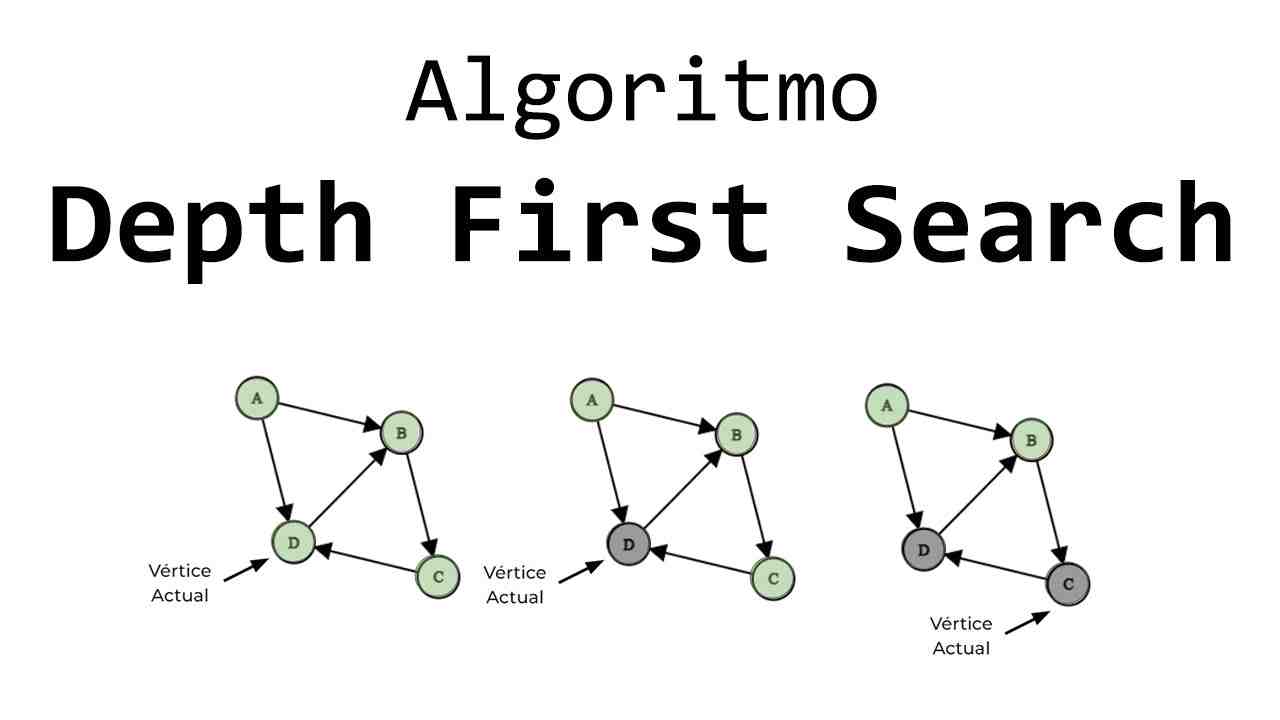
Búsqueda en Profundidad (DFS)

El algoritmo de búsqueda en profundidad (DFS) explora un grafo comenzando desde un nodo raíz y explorando tanto como sea posible a lo largo de cada rama antes de retroceder. Esto se puede implementar utilizando una estructura de pila, ya sea de forma explícita o mediante la recursión. Una de las principales características de DFS es que puede ser más eficiente en términos de uso de espacio, ya que no necesita almacenar todos los nodos a la misma profundidad al mismo tiempo. Sin embargo, una desventaja importante es que puede quedarse atrapado en ciclos si no se implementa un mecanismo de control que evite visitar el mismo nodo varias veces.

DFS es especialmente útil para problemas como la detección de ciclos en un grafo y la búsqueda de caminos en laberintos, donde se necesita explorar grandes y complejas estructuras. Por ejemplo, al buscar un camino en un laberinto representado como un grafo, DFS puede encontrar una solución más rápidamente al seguir una ruta hasta llegar a un callejón sin salida y luego retroceder para explorar otras posibles rutas.

Búsqueda en Amplitud (BFS)

El algoritmo de búsqueda en amplitud (BFS), por otro lado, explora el grafo nivel por nivel. Comenzando desde un nodo raíz, BFS investiga todos los nodos vecinos a ese nivel antes de pasar a los nodos del siguiente nivel. Este enfoque garantiza que se encuentre el camino más corto en un grafo no ponderado, lo que lo convierte en una excelente opción para problemas como el recorrido de redes o la navegación en mapas. Para implementar BFS, se utiliza una cola que ayuda a gestionar el orden de exploración de los nodos.

Una de las aplicaciones más conocidas de BFS es en las redes sociales, donde se busca la conexión más corta entre dos usuarios. Si un usuario A quiere encontrar el usuario B, BFS puede determinar el nivel de conexiones en el que se encuentra, permitiendo conocer la distancia en términos de amigos mutuos. Esto no solo es útil en redes sociales, sino también en aplicaciones de logística para determinar rutas óptimas en redes de transporte.

Optimización de Algoritmos de Búsqueda

Para mejorar la eficiencia de los algoritmos de búsqueda, se han desarrollado varios métodos de optimización. Por ejemplo, el algoritmo A es una variante avanzada que combina la búsqueda en amplitud con una función heurística que puede guiar la búsqueda hacia la solución más rápidamente. A se utiliza frecuentemente en áreas como la inteligencia artificial y la programación de juegos para la planificación de movimientos y decisiones en entornos complejos.

Además, la utilización de estrategias de poda, como el algoritmo de sucesor, permite disminuir el número de nodos que se deben explorar. Esto es particularmente efectivo en problemas donde existen muchas ramas, ya que evita el cálculo innecesario de rutas que son evidentemente subóptimas. Por lo tanto, el correcto uso de estas optimizaciones puede mejorar el rendimiento de los algoritmos de búsqueda, haciéndolos más aplicables a problemas a gran escala.

Aplicaciones Prácticas de los Algoritmos de Búsqueda en Grafos

Los algoritmos de búsqueda en grafos tienen aplicaciones en una variedad de campos. En tecnología, se utilizan en motores de búsqueda para rastrear e indexar páginas web. Este proceso es esencial para ofrecer resultados de búsqueda precisos y relevantes. Además, los algoritmos de búsqueda ayudan a las plataformas de redes sociales a gestionar la información y las interacciones entre usuarios, creando un entorno más intuitivo y accesible para la comunidad.

En biología, los algoritmos se utilizan para modelar interacciones entre proteínas y en estudios de redes metabólicas, cruciales en la investigación de enfermedades y el desarrollo de tratamientos. En logística, optimizan rutas de entrega, reduciendo los costos y mejorando la eficiencia del transporte. Por ejemplo, las empresas de mensajería suelen usar algoritmos de búsqueda en grafos para encontrar rutas optimizadas que satisfagan múltiples entregas en el menor tiempo posible.

Desafíos y Futuro de los Algoritmos de Búsqueda en Grafos

A pesar de su gran utilidad, los algoritmos de búsqueda en grafos enfrentan varios desafíos. Algunos de estos incluyen el crecimiento exponencial de la complejidad que presentan los grafos, especialmente en aplicaciones a gran escala como la inteligencia artificial y la optimización de redes. Esto puede llevar a tiempos de ejecución prolongados, lo que requiere el desarrollo de nuevas técnicas y algoritmos más eficientes.

El futuro de los algoritmos de búsqueda en grafos está indudablemente relacionado con avances en áreas como el aprendizaje automático, donde se utilizan para optimizar modelos y procesos. Con la creciente interconexión de datos y la complejidad de los grafos que representan las relaciones entre esos datos, se espera que los algoritmos de búsqueda continúen evolucionando, mejorando su capacidad para proporcionar soluciones rápidas y efectivas a problemas que aún hoy en día permanecen sin resolver.

Conclusión

Los algoritmos de búsqueda en grafos son herramientas poderosas que nos permiten comprender y optimizar las relaciones entre diferentes elementos en un conjunto vasto de aplicaciones. Desde la búsqueda en profundidad y amplitud hasta optimizaciones como el algoritmo A, cada método ofrece ventajas específicas adecuadas para diversas áreas de aplicación. Con la creciente complejidad de los datos y la interconexión de la información, es crucial seguir investigando y desarrollando estos algoritmos, asegurando que podamos enfrentar los desafíos del futuro de manera efectiva. La comprensión de estas técnicas no solo es valiosa para los profesionales del área tecnológica, sino que también tiene implicaciones en numerosos campos que dependen de la gestión y análisis de redes complejas.